模型结构
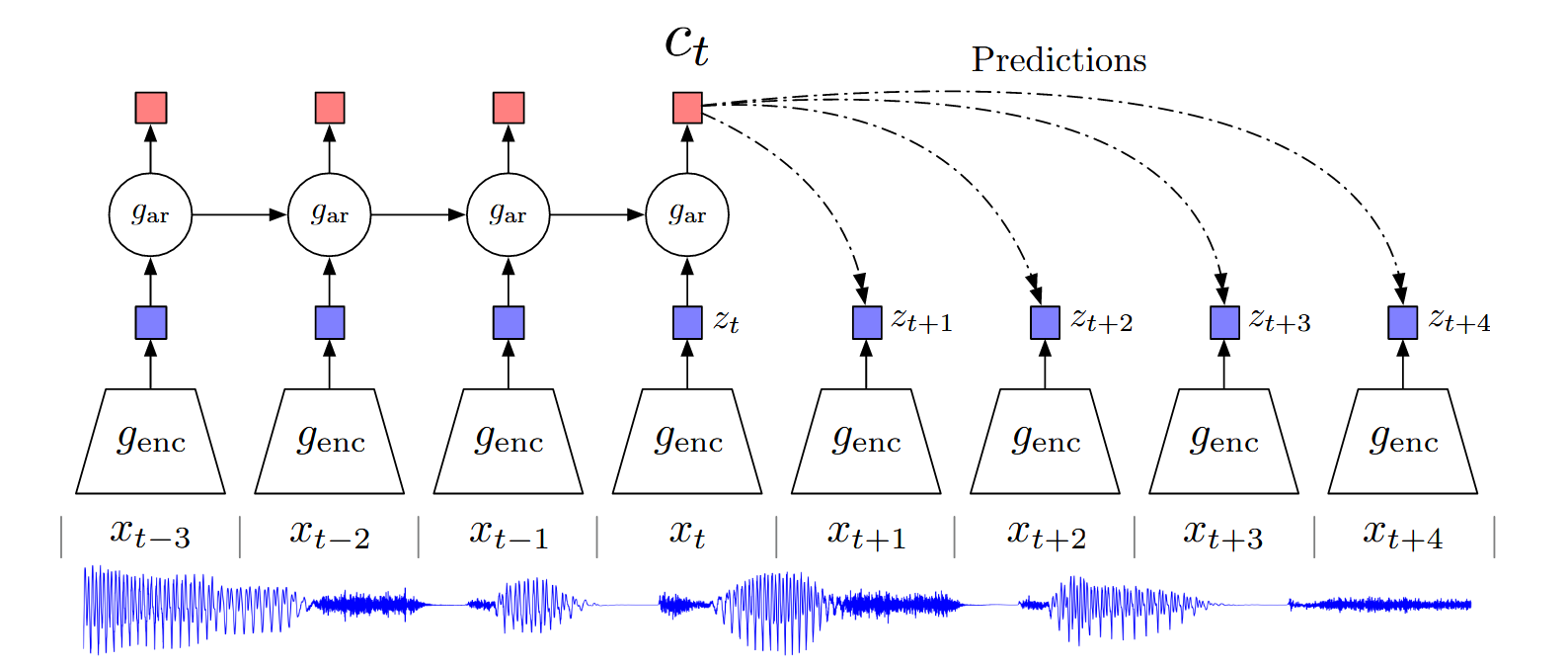作者使用g_{enc}编码器（5层CNN+ReLU）对输入信号x进行编码得到z ，再使用自回归模型g_{ar} （一层GRU+RNN）编码历史时刻的隐变量z得到上下文特征 c_t，然后作者利用c_t 去预测z_{t+k} ，最终的目标就是让\hat{z}_{t+k} 与z_{t+k} 之间的差异最小的同时，又与其他不同的信号序列的z'_{t+k} 差异尽可能小。这就是作者对比学习的思路。
损失函数
作者基于NCE提出一种叫做InfoNCE的对比学习损失函数。这里要提一个概念，互信息，它表示两个变量之间的相关性，I(X;Y)表示X 与Y 的互信息。在论文中，最大化I(x|c)来使得模型充分学习现在上下文c 的信息来使得未来x 的不确定性减小，从而起到预测效果，作者证明了最小化InfoNCE损失等价于最大化上述互信息I(x|c) 的一个下界。
这个InfoNCE损失的公式为：
\mathcal{L}_N: 损失函数的符号，用于最小化模型在预测未来时的不确定性。
\mathbb{E}_X: 期望符号，X代表输入数据集中的样本。
z_{t+k} : 这是目标数据的特征向量，表示时间步t+k的潜在特征表示。
W_k : 这是预测参数矩阵，用于将上下文向量c_t映射到目标空间。
\sum_{x_j \in X} : 对数据集中的负样本进行求和。
InfoNCE损失通过最大化正样本（即真实的未来时间步）和上下文的相似性，以及最小化负样本（随机采样的其他样本）和上下文的相似性，来逼迫模型学习出具有预测性的特征。
在这个公式中：
分子\exp(z_{t+k}^T W_k c_t)是希望最大化的正样本的得分。
分母中的所有项包括了多个负样本以及正样本，目的是通过对比的方式让正样本与负样本更容易区分。
这个损失函数对每个正样本都构建了一个对比任务，即希望模型能够输出正样本比负样本有更高的相似度。值得一提的是，作者取j时为了编码方便遍历了所有样本，而没有跳过当前输入样本。