（个人理解，如有错误可在评论区指出）

摘要

作者提出了一种使用离散标签预测作为预训练任务的，用于音频（Audio）的通用自监督模型BEATs。其核心是通过Acoustic Tokenizer（用于打标签）与Audio SSL Model（用于预测遮盖的标签）互相指导、迭代学习。作者在附录部分通过EM算法思想证明了这一过程的收敛性。

注：EM算法的作用，解决“先有鸡”还是“先有蛋”的问题

关键词

音频、自监督学习

背景

现状

近年来，语音（Speech）自监督（SSL）模型取得很多进步，如Wav2vec 2.0，HuBERT，BigSSL，WavLM，data2vec，但是也有论文指出，将语音自监督模型直接应用于Audio（音频）领域并不是非常合适，需要更通用的Audio领域的自监督模型。

前人的自监督模型根据预训练任务可以大致分成两类

  • （1）对输入音频数据进行随机掩蔽然后预测，这类通常采用的是声学特征重构损失作为预训练目标（应用于Audio）

  • （2）使用离散标签预测作为预训练任务（应用于Speech）

在本文提出之前，目前音频自监督的SOTA是（1）类型，但是论文的观点是（2）类型的任务离散标签预测可能是比重建更好的音频预训练目标。理由有三：

  • 人类通过提取和聚类高级语义来理解音频，而不是关注低级时频细节；

  • 离散标签预测目标可以通过提供语义丰富的标记作为预训练目标，并鼓励模型丢弃冗余细节；

  • 有离散标签预测目标的音频SSL预训练促进了语言、视觉、语音和音频预训练的统一，并使得通过单一预训练任务（即离散标签预测）跨模态构建基础模型成为可能。

论文指出目前使用离散标签作为预训练任务的难点有两点，总结而言：

  • 音频信号的连续性

音频信号包含大量不同的非语言声学事件和环境声音（如汽车的声音、风声、鸟叫等），这些声音的变化范围比语音要大得多，不像Language Process、Speech等领域那样。

  • 音频信号包含的多样性

与语音不同，一般音频信号包含的数据变化非常大，包括各种非语音声学事件和环境声音。现有的语音自监督学习模型（如 HuBERT）通常使用的是用于提取音素信息的语音标记器（speech tokenizer），这些标记器专门设计用于语音中的音素提取。然而，语音标记器无法直接应用于一般音频信号，因为一般音频信号的多样性远远大于语音信号。

BEATs

为了解决上述提到的问题，作者提出了BEATs（Bidirectional Encoder representation from Audio Transformers），迭代音频预训练框架进行同时优化声学标记器和音频SSL模型。训练的pipeline如下所示：

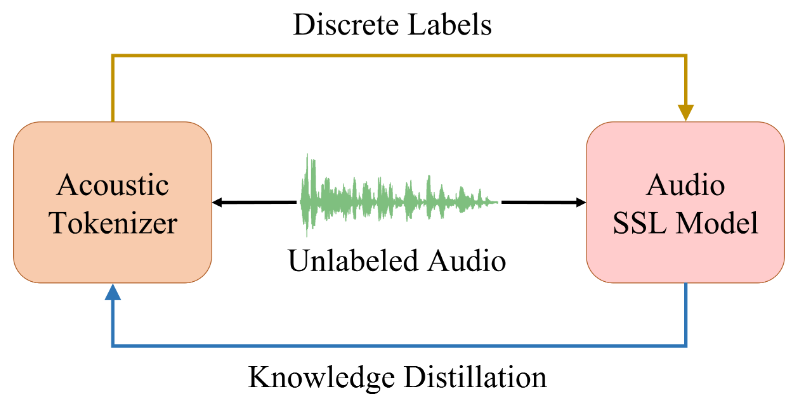
在每次迭代中，作者首先使用声学标记器来生成未标记音频的离散标签，并使用它们来优化带有掩码和离散标签预测损失的音频SSL模型。收敛后，音频SSL模型作为老师，引导声学标记器通过知识蒸馏学习音频语义。

具体来说，在第一次迭代中，使用随机投影声学标记器来生成离散标签作为冷启动，此外，可以使用少量的监督数据对音频SSL模型进行微调，并将微调后的模型用作声学标记器训练的老师。经过微调的模型不仅可以从SSL学习语义知识，还可以从监督学习中学习，这可以进一步提高标记器的质量。

作者使用原始的ViT模型作为音频SSL模型骨架。给定由声学分词器生成的离散标签，屏蔽75%的输入序列，并让模型在屏蔽区域上预测相应的离散标签。

BEATs预训练模型在六项音频和语音分类任务中表现优异，尤其在AudioSet-2M和ESC-50数据集上超越了之前的SOTA结果，显著提升了性能和效率。声学标记器生成的离散标签对随机干扰具有鲁棒性，并与音频语义高度对齐。

相关工作

与前人研究核心不同之一就是本文采用了Acoustic Tokenizers。用于学习音频和语音任务的离散表示已有各种不同的tokenizers（将连续的音频信号转换为离散表示，也称为“tokens”，类似于在NLP任务中，将文本划分为一个个单词或子词的标记器的工具）。可以概括如下：

VQ-VAE（Dieleman等人, 2018）

  • Tokenizer 类型：矢量量化变分自编码器（VQ-VAE）。

  • 作用：通过自编码（auto-encoding）的方式，将输入音频编码成低维的潜在表示（latent representations），然后通过量化（quantization）将这些潜在表示转换成一组离散tokens。这些tokens 可以用于生成音乐或其他音频任务。

  • 特点：VQ-VAE通过学习音频的潜在表示，并将其量化为有限数量的离散类。

HuBERT（Hsu等人, 2021）

  • Tokenizer 类型：基于聚类的标记器。

  • 作用：HuBERT通过迭代训练，使用早期模型生成的隐藏状态进行聚类，然后将聚类结果作为离散标签。新一轮的模型会根据这些离散标签进行训练。

  • 特点：聚类方法将连续的语音信号划分为多个语义类，模型需要学习这些离散类的模式。

随机投影标记器（Chiu等人, 2022）

  • Tokenizer 类型：随机投影标记器。

  • 作用：通过简单的随机投影将输入信号映射到更低维的空间，这些投影结果被用于生成离散表示。这种方法没有复杂的预处理或聚类过程，直接用随机方式生成tokens。

  • 特点：标记器相对简单，依赖于随机投影的生成过程。

BEATs

  • Tokenizer 类型：基于掩蔽离散标签预测的声学标记器。

  • 作用：BEATs通过前一轮的自监督学习模型生成音频信号的离散标签（tokens），并在下一轮模型中预测这些离散标签。不同于HuBERT的聚类方法，BEATs中的标记器是经过SSL模型监督训练生成的。

  • 特点：这是首次在更广泛的音频任务中使用掩蔽离散标签预测，这些tokens表示更高层的语义信息。

BEATs

我们这部分重点来说说这些个模块是怎么实现的，换句话来说，知道了理论，那具体结构呢？

1. 迭代的音频预训练

BEATs使用迭代训练的方法，其中包含两个部分声学标记器（第2节）和音频SSL模型（第3节）。在每次迭代中，给定未标记的音频，使用声学标记器生成标签，并使用它们来训练具有掩码和标签预测损失的音频SSL模型。在模型收敛后，使用音频SSL模型作为教师，用知识蒸馏训练一个新的声学标记器，用于音频SSL模型的下一次迭代训练。

也就是说，acoustic tokenizer先对音频贴标签，音频SSL模型是利用 acoustic tokenizer输出的信息进行训练，训练的内容是给部分遮住标签的数据进行预测标签，音频SSL模型收敛后指导acoustic tokenizer更准确的贴标签，不断循环往复。

2. Acoustic Tokenizers

声学标记器用于为BEATs预训练的每次迭代生成离散标签。在第一次迭代中，考虑到教师模型不可用，作者使用随机投影标记器（Random-Projection Tokenizer）将连续的声学特征聚类到离散的标签中作为冷启动。从第二次迭代开始，作者训练一个自蒸馏标记器（Self-Distilled Tokenizer），使用从上次迭代中获得的预训练/微调音频SSL模型中生成的标签。

冷启动 Tokenizers：Random-Projection Tokenizer

对于BEATs预训练的第一次迭代，我们应用随机投影标记器（Chiu et al., 2022）为每个输入音频生成补丁级离散标签。

何为补丁级？就是给一个固定时间长度t，把复数的帧按t长度分组，每组就是一个补丁级。

这个过程如图所示，下面有更详细的介绍。

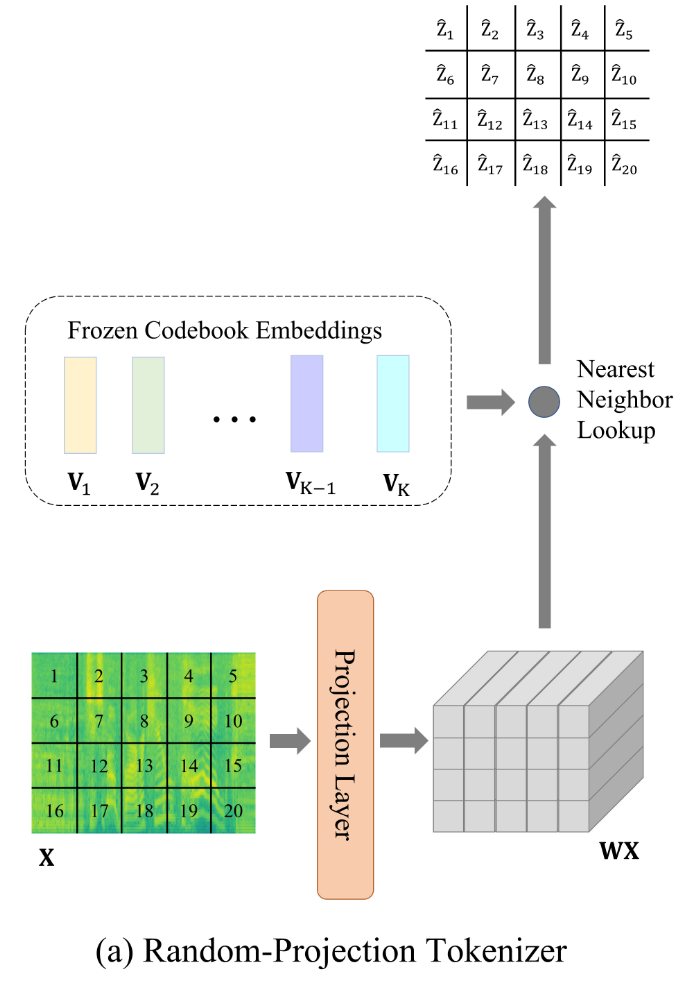
我们首先要明确这个无训练的Tokenizer贴标签的粒度，是对每个特征补丁而言的，并不是对每个音频进行贴标签。

算法步骤

1. 输入特征的提取

从输入音频中提取一系列特征补丁（patch sequence），表示为X = \{x_t\}_{t=1}^{T}，这里的特征补丁指的是根据一个固定的时间长度与频率长度将X 在两个维度上同时分组，得到一个个小矩阵，称之为特征补丁 。

2. 线性投影（Linear Projection）

首先，通过一个随机初始化的线性投影层 W将特征补丁 x_t 投影到一个新的向量空间中，计算公式为：

W x_t

这个过程类似于线性变换，将输入特征投影到一个新的维度，生成一组新的特征表示。

3. 查找最近邻向量（Nearest Neighbor Search）

接下来，为了将每个投影后的向量 W x_t 转换为离散标签，需要从一个随机初始化的码本（codebook）中找到与该向量最近的邻居向量。码本中包含K个向量，表示为V = \{v_i\}_{i=1}^{K}，其中每个v_i是预先随机生成的。

对于投影后的向量 W x_t ，通过计算其与码本中所有向量的欧几里得距离，找到最近邻的向量v_i。公式为：

\hat{z_t} = \arg \min_i ||v_i - W x_t||_2^2

这里\hat{z_t}是与投影后的向量W x_t最近的码本向量的索引，定义为该特征补丁的离散标签。

4. 生成离散标签：

通过以上步骤，每个输入音频的特征补丁都会被分配一个码本中的离散标签。整个输入音频的特征补丁序列 X就生成了一个对应的离散标签序列\{\hat{z_t} \}_{t=1}^{T}。

算法特点

  • 线性投影层W和码本向量V都是随机初始化的，且在整个过程中保持冻结（即不进行训练）。这意味着整个标记器在冷启动阶段是非训练的，它依赖随机投影和最近邻查找生成初始标签。

简单来说该算法的核心在于通过最近邻搜索为每个输入特征补丁分配一个离散标签，提供初始的标签生成机制。

迭代 Tokenizers：Self-Distilled Tokenizer

先看模型结构

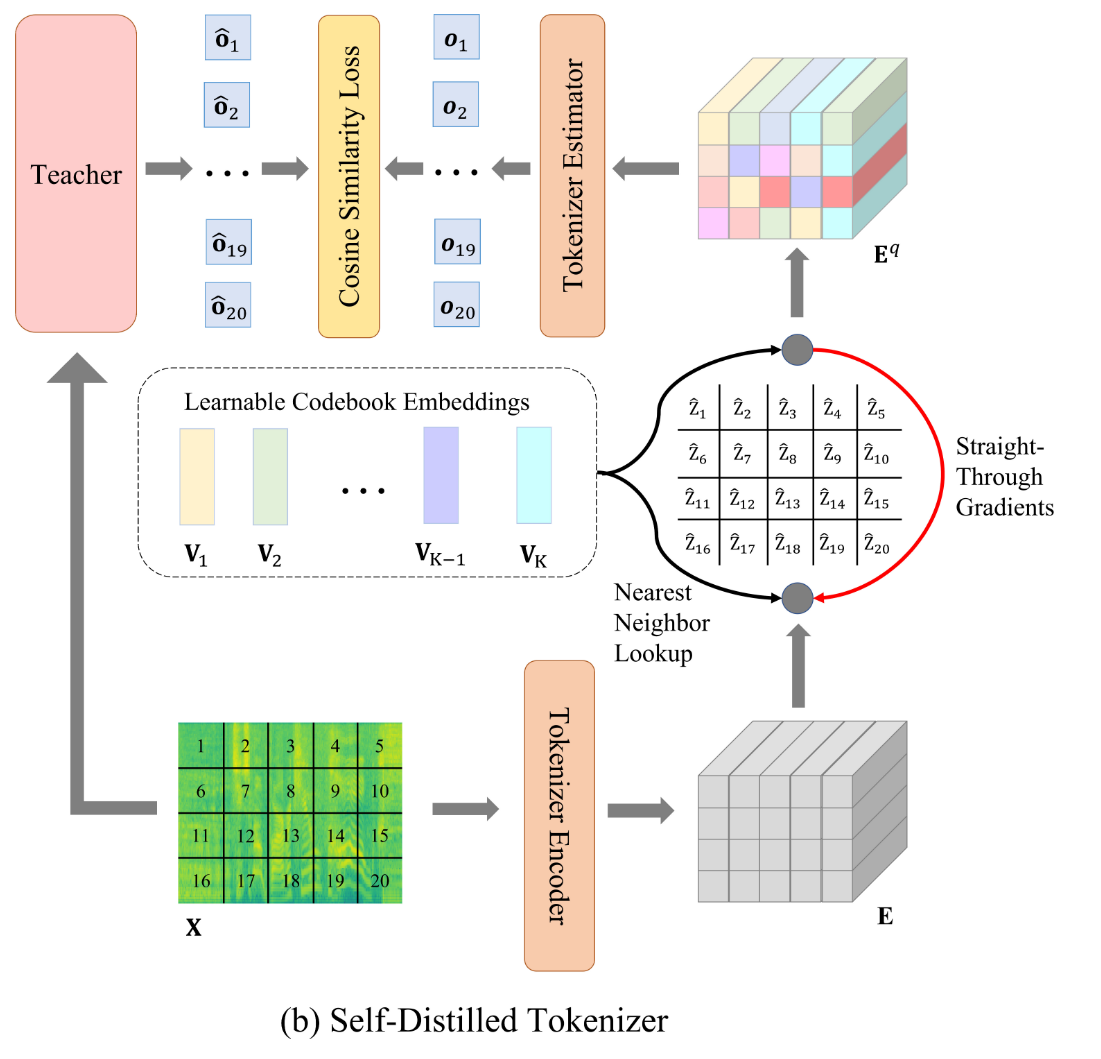
整个流程可以被如下描述

Start：

输入特征补丁，通过基于 Transformer 的标记器编码器获取特征补丁对应的embedding

如果是训练，使用上一轮SSL模型生成的标签数据

TrainStep1：

找到每个特征embedding在码本中最接近的码本向量，用该向量直接代替embedding

TrainStep2：

输入特征补丁的embedding序列，注意由于TrainStep1，此时的embedding序列中的每个元素都是码本向量，通过一个三层的Transformer标记器估计器预测教师模型的输出

如果是推理，目标是生成下一轮训练SSL模型要使用的标签

InferenceStep：

直接找到最接近embedding的码本向量的标签，作为预测结果用于SSL的训练

值得注意的是，直通梯度机制（在图中用红色箭头表示）确保了在量化（TrainStep1）过程中，即使量化步骤不可微分，梯度仍然可以从量化后的特征传播回未量化的编码向量 E。

在前向传播中，量化的操作使得离散标签无法直接进行反向传播计算，而直通梯度机制允许我们在反向传播时直接计算梯度，并更新编码器的参数。

3. Audio SSL Model

预训练阶段

也是先看结构

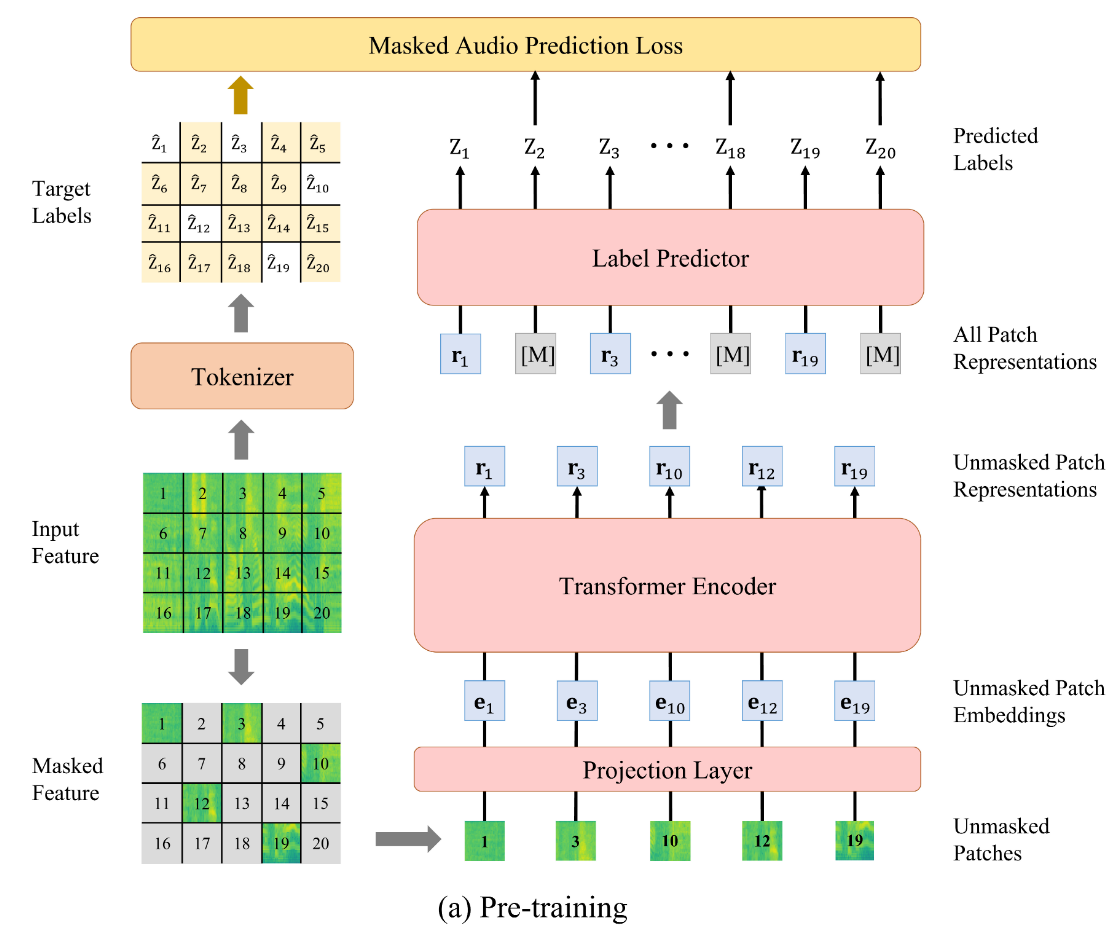
作者使用类似于ViT模型的骨架，预训练任务是Masked Audio Modeling (MAM)。具体来说，遮盖住75%的音频补丁，为每个补丁预测标签，这些大量的被遮盖的补丁预测时依赖于上下文语义信息，而并非自身的特征。

微调阶段

作者用一个简单的线性回归作为示例，这里可以替换成各种实际的下游任务。

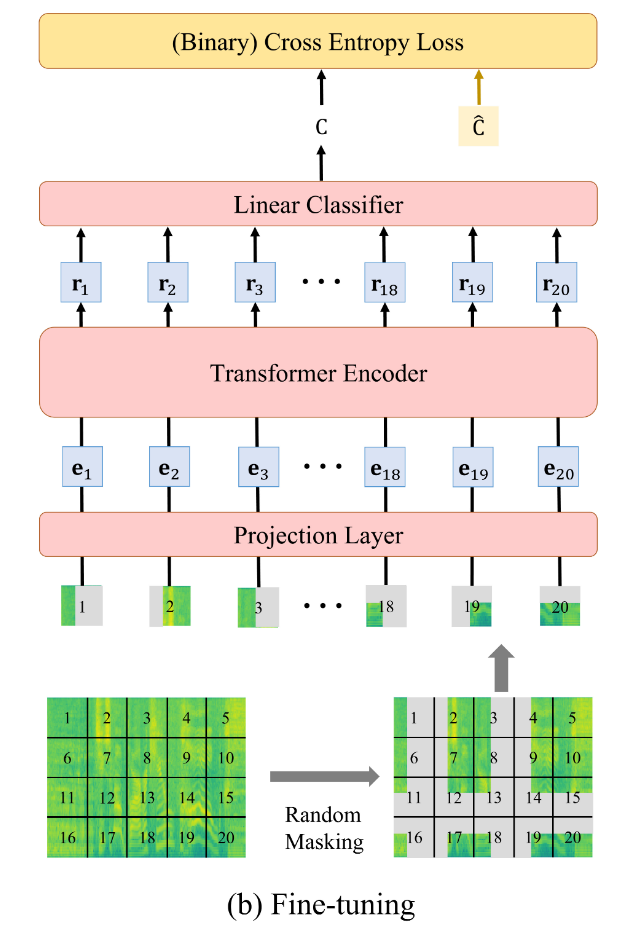
这个过程可以简单的总结为：

输入音频的随机遮盖

=>划分补丁并展平

=>将完整的补丁序列输入 ViT 编码器

=>线性分类器计算类别概率

=>使用交叉熵损失进行优化

附录

A 收敛性证明

整体思路

定义

X：输入音频样本

δ：标记器参数；Z：标记器打的离散标签

θ：SSL模型参数；R：SSL模型对数据提取出的特征表示

p(\mathbf{X} | \theta, \delta)：似然函数

整体的证明目标是说明p(\mathbf{X} | \theta, \delta)是随着训练轮数增加，是非递减的。

作者的证明分三步走，

A.1 \forall t \in \mathbb{N}, \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) \geq \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)}) ，这步说明在每轮训练声学标记器时，似然函数不降低；

A.2 \forall t \in \mathbb{N}, \log p(\mathbf{X} | \theta^{(t+1)}, \delta^{(t+1)}) \geq \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) ，这步说明在每轮训练音频自监督模型时，似然函数不降低；

A.3 \forall t \in \mathbb{N}, \log p(\mathbf{X} | \theta^{(t+1)}, \delta^{(t+1)}) \geq \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)}) ，这步说明在每轮训练整个模型时，似然函数不降低。

作者在A.1和A.2的证明中分别应用了EM算法思想，然后联立A.1和A.2得到A.3。

  • 为什么说似然函数不降低能体现模型性能不降低？

  • ==> 似然函数含义：一组参数θ, δ观测出数据为X的概率

    ==> 极大似然函数的过程，通过调整模型参数，来尽可能接近X的分布

    ==> Z 和 R 存在一个正确的真实值，但不可直接观测，我们只能得到估计值，它描述了数据的某种内部特征

    ==> 模型调整θ, δ去估计的分布越接近X，那么Z与R的计算越准确

    ==> 似然函数变大

    <=> （训练目标）模型性能变好

引理A.1

\forall t \in \mathbb{N}, \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) \geq \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)})

我们主要说明A.1的证明过程，A.2与之类似。

展开似然函数

\begin{align*} \log p(\mathbf{X} | \theta, \delta) &= \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \log p(\mathbf{X} | \theta, \delta) \\ &= \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \left( \log p(\mathbf{X}, \mathbf{R} | \theta, \delta) - \log p(\mathbf{R} | \mathbf{X}, \theta, \delta) \right) \\ &= \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \left( \log \frac{p(\mathbf{X}, \mathbf{R} | \theta, \delta)}{q(\mathbf{R})} - \log \frac{p(\mathbf{R} | \mathbf{X}, \theta, \delta)}{q(\mathbf{R})} \right) \\ &= \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \log \frac{p(\mathbf{X}, \mathbf{R} | \theta, \delta)}{q(\mathbf{R})} - \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \log \frac{p(\mathbf{R} | \mathbf{X}, \theta, \delta)}{q(\mathbf{R})} \\ &= \mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \log \frac{p(\mathbf{X}, \mathbf{R} | \theta, \delta)}{q(\mathbf{R})} + \text{KL}(q(\mathbf{R}) \| p(\mathbf{R} | \mathbf{X}, \theta, \delta)), \end{align*}

逐行注释：

行1：设定q(R)为R的真实分布。为什么选择R？因为训练声学标记器依赖R，依赖于上一轮SSL模型的输出。

行2：条件概率公式\frac{p(A, B)}{p(B)} = p(A | B)

行3：对数的性质\log\left(\frac{A}{C}\right) - \log\left(\frac{B}{C}\right) = \log(A) - \log(B)

行4：展开

行5：KL散度定义。其中\mathbb{E}_{\mathbf{R} \sim q(\mathbf{R})} \log \frac{p(\mathbf{X}, \mathbf{R} | \theta, \delta)}{q(\mathbf{R})} = \text{ELBO}(q(\mathbf{R}), \theta, \delta) ，是ELBO定义。

结论A.1.1

训练声学标记器的过程可以看作应用最大期望算法，先认为SSL模型输出的标签分布是正确的（E步），然后根据这个标签数据训练声学标记器的参数（M步）。

对于第t+1轮训练声学标记器的E步，认为上一轮R的后验分布是真实分布q(\mathbf{R})

形式化地，q(\mathbf{R}) = p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})

E步的目标可以看作是最小化\text{KL}(q(\mathbf{R}) \| p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})) ，这意味着训练声学标记器时的R的分布会向着q(\mathbf{R}) ，也就是上一轮训练完的SSL模型的R的分布对齐。

所以我们现在可以得到结论A.1.1

\mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t+1)}) = \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})

结论A.1.2

在(t+1)轮迭代，训练声学标记器的M步中，我们优化参数 \delta

应用E步的期望，KL最小（=证据下界最大）时，为新的 \delta

为什么说KL最小等价于证据下界最大？

我们回头看一开始似然函数最终的展开式，注意对于t+1轮训练声学标记器而言，E步中，\theta = \theta^{(t)}, \quad \delta = \delta^{(t)} 都是定值，所以\log p(\mathbf{X} | \theta, \delta)是定值，所以ELBO最大等价于KL最小

所以我们得到\delta^{(t+1)}表达式

\delta^{(t+1)} = \arg \max_{\delta} \text{ELBO}(p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)}), \theta^{(t)}, \delta) \\ = \arg \max_{\delta} \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log \frac{p(\mathbf{X}, \mathbf{R} | \theta^{(t)}, \delta)}{p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \\ = \arg \max_{\delta} \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X}, \mathbf{R} | \theta^{(t)}, \delta)

逐行解释：

行1：这行原本是\text{ELBO}(q(\mathbf{R}), \theta, \delta) ，M步中，认为q(\mathbf{R}) = p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)}) ，就有了这行

行2：展开ELBO

行3：展开变成\log \left( \frac{A}{B} \right) = \log A - \log B ，对于第二项而言，\delta^{(t)} 已经是个确定值，而我们在求\delta 取何值时能使表达式最大，故此项对结果无影响，是不含变量\delta 的项，可直接删去。

这里我们得到结论A.1.2

\mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X}, \mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t+1)}) \geq \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X}, \mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})

得出引理A.1

所以我们能得到引理A.1

\begin{align*} \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) &= \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) \\ &= \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \left( \log p(\mathbf{X}, \mathbf{R} | \theta^{(t)}, \delta^{(t+1)}) - \log p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)}) \right) \\ &= \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X}, \mathbf{R} | \theta^{(t)}, \delta^{(t+1)}) - \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)}) \\ &\geq \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X}, \mathbf{R} | \theta^{(t)}, \delta^{(t)}) - \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)}) \\ &= \mathbb{E}_{\mathbf{R} \sim p(\mathbf{R} | \mathbf{X}, \theta^{(t)}, \delta^{(t)})} \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)}) \\ &= \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)}) \end{align*}

逐行解释：

行1：明确R是从\theta^{(t)},\delta^{(t)} 两个参数所描述的分布中取的，即上一轮SSL模型的参数。

行2：运用条件概率公式进行展开

行3：展开

行4：此时是EM算法的E步，对第二项应用结论A.1.1，假设\theta^{(t)},\delta^{(t)} 参数下的分布就是真实分布，并在此假设下计算期望。

行5：此时是EM算法的M步，对第一项应用结论A.1.2，变为不等号，此时目标是找到能使得 ELBO 最大化的\delta^{(t+1)} ，\delta^{(t+1)} 所代表的似然不会低于之前的似然。

行6、7：将公式收回去

引理A.1得证

\forall t \in \mathbb{N}, \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t+1)}) \geq \log p(\mathbf{X} | \theta^{(t)}, \delta^{(t)})